Millman’s theorem & basic equivalences

Millman’s topology

A circuit that consists of all parallel connection of only the following type:

1. resistors
2. ideal current sources
3. series connections of and ideal voltage source and a resistor
   • Note resistors in series to the current source do not affect the Millman Voltage so we should not include it’s conductance in our calculations

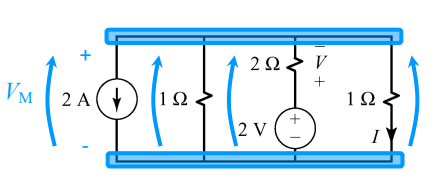
Millman’s theorem

\[V_m = \frac{[A] + [B]}{[C]}\]

Where:

$[A]$ = $\sum \pm G_kE_k$ for the branches with the voltage sources and resistors in series (positive is the voltage is in the same direction as the $V_m$

$[B] = \sum \pm A_k$ for the branches with current sources (positive if the direction of the current is the same as the $V_m$

$[C] = \sum $ condunctace of all resistors

Millman derived his theorem using a KCL at one of the two common nodes shared by the branches in a circuit of his topology type.

Examples

Source transformation

Two elements are equivalen if they have the same characteristic equation.

Typically:

• A voltage source with a resistor in series converts to a current source with a resistor in parallel.
• And vice versa, a current source with a resistor in parallel converts to a voltage source with a resistor in series.