Summary

• Series resistors
• Parallel resistors
• Current divider
• Voltage divider
  • $I_k = I_s \cdot \frac{G_k}{\sum\limits_{n} G_n}$

Ex 1

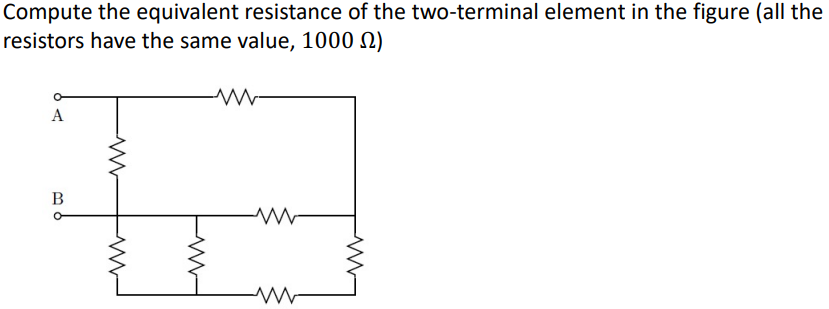
Answer

Ans: $\frac{12}{19}R$

Ex 2

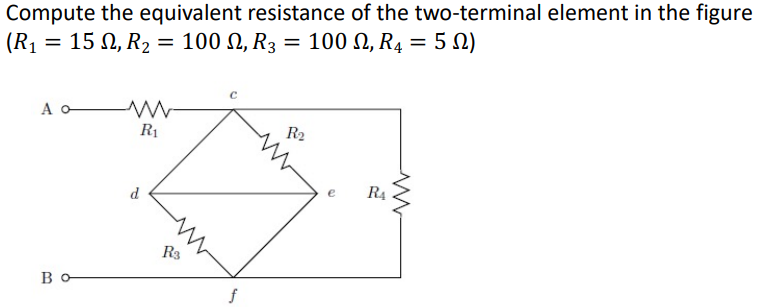
Answer

Ans: $R_{eq}$ = $R_1$

Because there is a short circuit from $c$ to $f$ passing by nodes $d$ & $e$

Ex 3

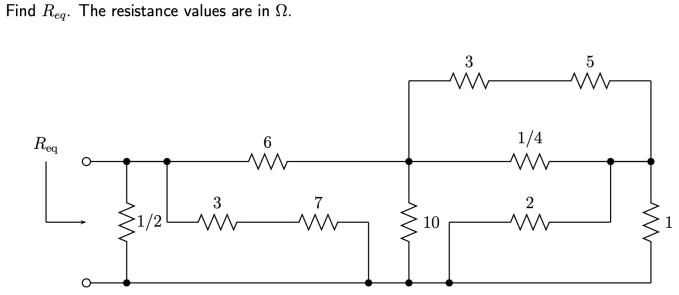
Answer

Ans: $R_{eq}$ = $0.44 V$

Ex 4

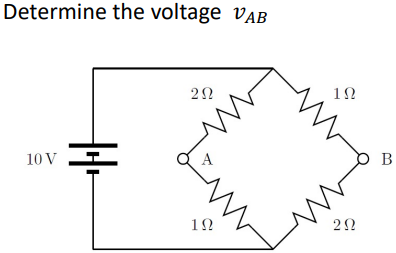
Working Out

Use voltage dividor to figure out the individual Voltages accross the resistances and then add them up between B and A in the direction from B to A.

This would mean that you take the negative voltage of the bottom $2\Omega$ resistor and plus the positive voltage of the bottom $1\Omega$ resistor.

$\therefore -\frac{10V}{\frac{2}{3}} + \frac{10V}{\frac{1}{3}} = -\frac{20V}{3} + \frac{10V}{3}$

Answer

Ans: $v_{AB}$ = $-\frac{10}{3}V$

Ex 5

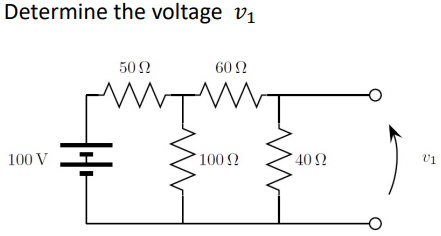
Working Out

Use resistor simplifying to find out how much voltage makes it beyond the $50\Omega$ resistor. Then use potential dividor to figure out the voltage accross $v_1$

$\therefore R_{eq}$ of the $100\Omega, 60\Omega, 40\Omega$ resistors. $R_{eq} = 50\Omega$ (Since the $60\Omega$ and the $40\Omega$ are in series so they simplify to $100\Omega$. Then you have two $100\Omega$ resistors in parallel which gives an $R_{eq}$ of $50\Omega$.

Using potential divider of the two $50\Omega$ resistors you get that $50V$ go accross the $R_{eq}$ circuit.

Using potential divider again (with the $60\Omega$ and $40\Omega$ resistors) you get that $20V$ go accross the $40\Omega$ resistor.

$\therefore v_1 = 20V$

Answer

Ans: $v_1$ = $20 V$

Ex 6

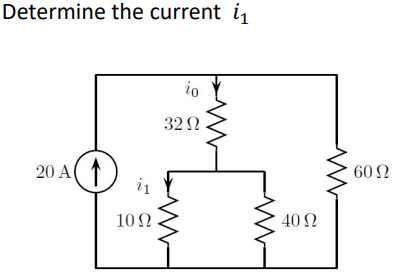
Working Out

Answer

Ans: $i_1$ = $9.6 A$

Ex 7

Working Out

Answer

Ans: V = $-\frac{9}{2}V$ and $\frac{1}{8}A$

Electrons are smart!