Normal Distribution
Normal Distribution
DEFINITION:
$X \sim N(\mu, \sigma)$ represents a normal distribution, where:
- $\mu =$ mean
- $\sigma =$ standard deviation
$P(X\ge x) = \Phi(z)$
\[\Phi(z) = \dfrac{1}{\sqrt{2\pi}} \int^z_{\infty} e^{\frac{-t^2}{2}} dt\]Calculating z
DEFINITION:
$z = \dfrac{x - \mu}{\sigma} \quad$ where:
- $x =$ individual value
- $\mu =$ mean
- $\sigma =$ standard deviation
Normal Distribution Table
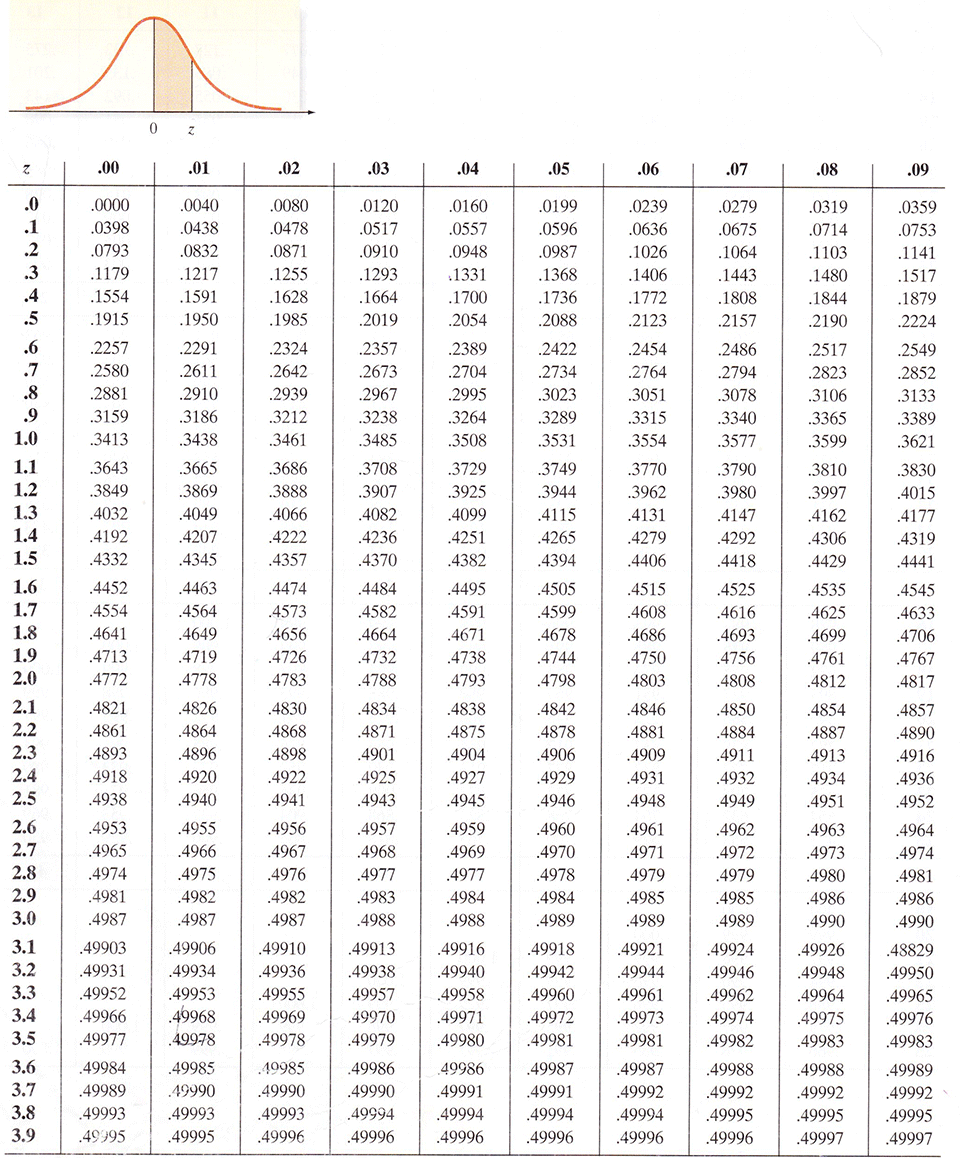
Used with the z value that was shown how to be calculated above.
The Empiricals
-
68% of the data lies between $\pm 1\sigma$ of $\mu$
-
95% of the data lies between $\pm 2\sigma$ of $\mu$
-
99.7% of the data lies between $\pm 3\sigma$ of $\mu$